Stochastic Perturbations of Tabular Features for Non-Deterministic Inference
With Automunge

Abstract
Injecting gaussian noise into training features is well known to have regularization properties. This paper considers noise injections to numeric or categoric tabular features as passed to inference, which translates inference to a non-deterministic outcome and may have relevance to fairness considerations, adversarial example protection, or other use cases benefiting from non-determinism. We offer the Automunge library for tabular preprocessing as a resource for the practice, which includes options to integrate random sampling or entropy seeding with the support of quantum circuits for an improved randomness profile in comparison to pseudo random number generators. Benchmarking shows that neural networks may demonstrate an improved performance when a known noise profile is mitigated with corresponding injections to both training and inference, and that gradient boosting appears to be robust to a mild noise profile in inference, suggesting that stochastic perturbations could be integrated into existing data pipelines for prior trained gradient boosting models.
1. Introduction
Stochasticity in the context of machine learning application can originate from many sources, often by design owing to corresponding regularization effects. This paper focuses on a particular kind of stochasticity associated with the injection of isotropic noise into the features of a tabular data set as passed to inference. Injecting noise into tabular features is not new, and we will survey several channels of inquiry dating back at least to the 1980’s. However most of these investigations have focused on injecting noise into the features of a training data set for purposes of model characteristics. One of the premises of this paper is that the non-determinism realized from injecting noise into features passed to inference can realize benefits adjacent to a primary performance metric.
Noise injections to features translate inference from a deterministic operation to sampling from a distribution. And because the injections are applied to the input features, the sampled noise distributions are translated to the inference distribution as a function of network properties as opposed to what would result from applying noise directly to the output of inference, using the model as a source of probabilistic programming. Sort of a free lunch. Noise injections to neural network training features can be expected to improve a master performance metric and prepare the model for a corresponding noise applied to test data features. While mainstream practice for tabular learning commonly prefers gradient boosting, it has recently been shown that even simple multi-layer perceptron neural networks are capable of outperforming gradient boosting for tabular learning with a proper regularization tuning regime (Kadra et al., 2021). As we will show through benchmarks, gradient boosting appears to be robust to a mild noise profile in inference, suggesting that noise could be integrated into existing pipelines of prior trained gradient boosting models [App F.10].
We briefly highlight here a few potential benefits for non-deterministic inference. We believe fairness considerations may be one example, as protected groups will as a result be exposed to a broader range of possible inference scenarios, each centered around the master model basis, and without eliminating trajectories (Rodriguez et al., 2021). Although there are other forms of mitigation available, the probabilistic aspects of non-deterministic inference can be applied without knowledge or identification of protected attributes. (If direction of transience is a concern, inference can also be run without noise to establish a border.) Another benefit is a robust protection against adversarial examples (Cohen et al., 2019), as a targeted inference sample will not have prior knowledge of what perturbations will be seen by the model. We expect that there are many other scenarios and use cases where non-deterministic inference should be considered as the default. This paper’s focus will primarily be for surveying practical considerations of how to implement.
One of our key contributions is the provision of the Automunge library (Authors, 2021b) as a resource for stochastic perturbation application, which also serves as a platform for tabular learning that translates tidy data (Wickham, 2014) to encoded dataframes for input to machine learning.
2. Automunge
Automunge (Teague, 2021b) is an open source python library, available now for pip install, built on top of Pandas (McKinney, 2010), Numpy (Harris et al., 2020), SciKit-learn (Pedregosa et al., 2011), and Scipy (Virtanen et al., 2020). It takes as input tabular data received in a tidy form, meaning one column per feature and one row per sample, and returns numerically encoded sets with infill to missing points, thus providing a push-button means to feed raw tabular data directly to machine learning. The extent of derivations may be minimal, such as numeric normalizations and categoric binarizations under automation, or may include more elaborate univariate transformations, including aggregated sets thereof. Generally speaking, the transformations are performed based on a fit to properties of features in a designated training set, and then that same basis may be used to consistently and efficiently prepare subsequent test data, as may be intended for use in inference or for additional training data preparation.
The interface is channeled through two master functions, automunge(.) and postmunge(.). The automunge(.) function receives a training set and if available also a consistently formatted test set, and returns a collection of dataframes intended for training, validation, and inference — each of these aggregations further segregated into subsets of features, index, and label sets. A validation set, if designated by ratio of partitioned data from the training set, is segregated from the training data prior to transformations and then consistently prepared on the train set basis to avoid data leakage between training and validation. The function also returns a populated python dictionary, which we call the postprocess_dict, recording steps and parameters of transformations. This dictionary may then be passed along with subsequent test data to the postmunge(.) function for consistent preparations on the train set basis, as for instance may be applied sequentially to streams of data. Because it makes use of train set properties evaluated during a corresponding automunge(.) call instead of directly evaluating properties of the test data, preparing data in the postmunge(.) function can be very efficient.
There is a built in extensive library of feature encodings to choose from. Numeric features may be assigned to any range of transformations, normalizations, and bin aggregations. Sequential numeric features may be supplemented by proxies for derivatives (Teague, 2020a). Categoric features may be encoded as ordinal, one hot, binarization, hashing, or even parsed categoric encoding (Teague, 2020b) with an increased information retention in comparison to one hot encoding by a vectorization as a function of grammatical structure shared between entries. Categoric sets may be collectively aggregated into a single common binarization. Categoric labels may have label smoothing applied (Szegedy et al., 2016), or fitted smoothing where null values are fit to class distributions. Sets of transformations to be directed at targeted features can be assembled which include generations and branches of derivations by making use of our family tree primitives (Teague, 2021b), as can be used to redundantly encode a feature in multiple configurations of varying information content. Such transformation sets may be accessed from those predefined in an internal library for simple assignment or alternatively may be custom configured. Even the transformation functions themselves may be custom defined from a very simple template. Through application statistics of the features are recorded to facilitate detection of distribution drift. Inversion is available to recover the original form of data found preceding transformations, as may be used to recover the original form of labels after inference. Missing data is imputed by auto ML models trained on surrounding features (Teague, 2021a).
3. Noise Injection Options
Noise sampling in the library is built on top of Numpy’s (Harris et al., 2020) np.random module which returns an array of samples, where samples from a Bernoulli distribution could be an array of 0’s and 1’s, or samples from a Gaussian could be an array of floats. The sampling operation accepts parameters consistent with their distribution (e.g. for Gaussian mean and scale), and also a specification for shape of returned samples, which we match to the shape of the feature for targeted injection. The Appendix [Appendix A] further surveys detail of library options, associated parameters, demonstrates application, and surveys more advanced noise profile composition techniques.
3.1 Numeric
For numeric injections, noise can be applied on a scaled version of the feature which allows for specification of distribution parameters independent of feature properties — e.g. when diverse numeric features are z-score normalized with a mean of 0 and a standard deviation of 1 then a noise profile can be specified independent of feature properties. In an alternate configuration, noise can be applied to an unscaled feature with noise scale adjusted based on evaluating the feature’s training set distribution. For noise injection to a z-score normalized feature the multiplication of columns for sampled Bernoulli (with 0/1 entries) and Gaussian (with float entries) results in Gaussian noise injected only to entries targeted based on the Bernoulli sampling, or a common application can be applied to inject in every entry by just replacing the Bernoulli sampling with a set of 1’s. The library implementation for sampling adjacent to a Bernoulli varies slightly by only sampling entries corresponding to Bernoulli activations to reduce the entropy seeding budget.
(normalized) + (Bernoulli) ∗ (Gaussian) = (injected)
We have not seen in prior literature the integration of a preceding Bernoulli sampling into a noise profile, so this might be considered another contribution of this paper. In benchmarking, smaller Bernoulli ratios allowed the model to tolerate a much larger scale of Gaussian noise before significant performance degradation, suggesting that in the language of information theory (Shannon, 1948) the entropy power of the noise distribution can be managed across both axes of scale and injection ratio.
The Gaussian sampling can also be replaced with different distribution shapes, like Laplace or Uniform. The Laplace distribution, aka the double exponential distribution, has a sharper distribution peak than Gaussian, meaning more samples will be within close proximity to the mean, but also thicker tails, meaning more outlier entries may be sampled [Fig 1]. In fact one way to think about it is that exponential tails can be considered as a kind of boundary between what would be considered thin or thick tails in other distributions (Cook, 2019). Thick tails refers to univariate distributions in which the aggregate measured statistics may be strongly influenced by a small number of, or even one, sampled outliers due to increased potential for extreme outliers (Taleb, 2020), where the prototypical example would be a power law distribution. A common characteristic of thick tails are increased kurtosis which refers to steepness of peak at central mode. Injecting noise with thicker tails has benefit of exposing inference to a wider range of possible scenarios that still has noise centered to an entry, albeit at a tradeoff that number of samples needed for the noise profile to align with the target distribution climbs with tail thickness (Taleb, 2019). We expect there may prove to be benefit of other noise profile distributions in certain applications, this is an open area for future research. We did not attempt to benchmark white noise.

The numeric injections may have the potential to increase the maximum value found in the returned feature set or decrease the minimum value. In some cases, applications may benefit from retention of such feature properties before and after injection. When a feature set is scaled with a normalization that produces a known range of values, as is the case with min-max scaling (which scales data to the range between 0–1 inclusive), it becomes possible to manipulate noise as a function of entry properties to ensure retained range of values after injection [Appendix H] [Alg 1]. Other normalizations with a known range other than 0–1 (such as for ‘retain’ normalization (Teague, 2020a)) can be shifted to the range 0–1 prior to injection and then reverted after for comparable effect. As this results in noise distribution derived as a function of the feature distribution, the sampled noise mean can be adjusted to closer approximate a zero mean for the scaled noise [Appendix H] [Alg 2].
3.2 Categoric
The injection of noise into categoric features is realized by sampling from discrete distributions. For boolean integer categoric sets (as is applied to features with 2 unique values in our ‘bnry’ transform), in one configuration the injection may be applied by directly applying a Bernoulli 0/1 sample to flip targeted activations, although our base configuration applies comparable approach as ordinal encodings to take advantage of weighted replacements.
abs((boolean) − (Bernoulli)) = (injected)
For categoric sets, after ordinal encoding a Bernoulli (0/1) sampling may select injection targets and a Choice sampling select alternate activations from the set of unique entries for the feature found in the training data.
(ordinal)∗(1−(Bernoulli))+(Choice)∗(Bernoulli) = (injected)
In our base configuration, the sampling of alternate activations is weighted by frequency of those activations as were found in the training data, and number of Choice samples is instead based on number of Bernoulli activations.
Having injected noise, a downstream transform can then be applied to convert from ordinal to some other form, or the same kind of noise can be injected downstream of a transform that reduces the number of unique entries like a hashing. We have additional configurations for categoric injections, like those applied with one hot, binarization, or multi-column hashings, that can directly be applied downstream of multi-column categoric encodings or downstream of a set of single column encodings for similar results.
3.3 Neutral
A type of noise profile that can be applied consistently to both numeric and categoric features is known as swap noise (Ucar et al., 2021). Swap noise refers to the practice of, for Bernoulli sampled entry injection targets, replacing that entry with a Choice sampling from all entries of the same feature. One way to think about swap noise is that it is sampling from the underlying distribution of the feature. As implemented in the library, swap noise can be applied in same fashion to either single or multi column encodings. For categoric features, it has a similar result as the weighted choice sampling noted above. A tradeoff is that for injections to test data in inference the sampled swap noise is based on the test feature distribution and thus potentially exposed to covariate shift, or for inference with a small number of samples that distribution may be underrepresented.
Another noise type that is neutral to feature properties is known as mask noise, and simply refers to replacing Bernoulli sampled entry targets with a mask value, like 0.
4. Random Sampling
The sampling performed by numpy.random first draws numbers from a uniform distribution which is then converted to a shaped distribution. The sampling is realized with a pseudo random number generator and currently defaults to the PCG (O’Neill, 2014) algorithm (having recently replaced the Mersenne twister (Matsumoto & Nishimura, 1998) generator used in earlier implementations). While these types of generators are not considered on their own validated for cryptographic applications due to their use of deterministic algorithms, they have statistical properties that resemble randomness (hence the name pseudo random number generator). They generally attempt to circumvent determinism by incorporating some form of external entropy seeding into application, which in common practice is accessed from a resource in the operating system for this purpose, and may draw from such fluid channels as local memory or clock states that are known to have properties resembling randomness. In one configuration a single seed may be used to initialize a sampling operation with the remainder of samples drawn based on the progression of the generator, in an alternate configuration each sampled value may have a distinct external seed, which second configuration may have latency tradeoffs.
One of the the numpy.random generator features that the Automunge library takes advantage of is for the incorporation of supplemental entropy seeds into a sampling operation. The purpose of supplemental seeds are to access additional entropy sources other than those that may be available to the operating system for purposes of an enhanced randomness profile. Automunge has a few seeding configurations to choose from, where the quantity of seeds needed to support any of these configurations are provided to the user in a returned report [App F.7]. In one potential workflow the report may be generated by preparing a subset of the data without seeding, and then preparing the full data with seeding based on the reported quantity of seeds needed for any of these scenarios. The report details seed requirements for both train and test data so that once established the basis is known for inference. The entropy seeding scenarios are available by ‘sampling type’ specification as follows:
- default: every sampling receives a common set of seeds which are shuffled and passed to each call
- bulk_seeds: every sampled entry receives a unique supplemental seed
- sampling_seed: every set of sampled entries receives one unique supplemental seed
- transform_seed: every noise transform receives one unique supplemental seed
In the the bulk seeds configuration external entropy seeds are used as the only source of seeding, as opposed to the other sampling type scenarios where it is combined as a supplemental seed to those sourced from the operating system.
As an alternative to, or in addition to, externally sampled entropy seedings, a user may also provide an alternate random number generator to be applied in place of the PCG default. The generator may be accessed from the numpy.random library (Harris et al., 2020), or may be an external library that adheres to the numpy.random.Generator format. In one configuration, the alternate generator may channel sampling operations through a quantum computing cloud resource (Rivero, 2021).
In another supported configuration, a quantum computer may be accessed as an external source of entropy for supplemental seeds to be channeled through the default PCG generator, which has the benefit of intentional sampling type specification for budgetary considerations associated with accessing the cloud resources. When channeling external entropy seeds, the default configuration is that the seeds are added as supplemental seeds alongside those sourced from the OS, with exception of the bulk seeds case where external seeds are used as the only form of seeding.
5. Quantum Sampling
Quantum computers (Nielsen & Chuang, 2010) have an inherent advantage over classical resources for accessing more pure random states, without the need to overcome the deterministic nature of pseudo random number generation or whatever structures might be found in sources of entropy seeding. Put differently, quantum entropy is closer to i.i.d. (Piani et al., 2021).
A quantum circuit is realized as a set of qubits, as are often initialized in the |0⟩ state, that are manipulated into a joined superposition by application of quantum gates, and then a measurement operation returns a classical state from the qubits, with each probabilistically collapsing to either 0 or 1 as a function of the superposition and measurement angle. In the terminology of cloud vendors, each superposition preparation and corresponding set of measurements is considered a shot, which often serves as a pricing basis. In many quantum machine learning applications, such as for tuning the parameterized gates of a quantum neural network (Broughton et al., 2021), an algorithm may require a large number of shots to refine gate configurations from a gradient signal. When quantum circuits are applied for random number sampling, each sampled entry may only require a single or few shots to extract the desired output.
There are several types of quantum circuits that can be applied for sampling. In the simplest configuration known as the Hadamard Protocol, a single H gate is applied to each qubit, which places them in an equal superposition between |0⟩ and |1⟩ as the superposition (|0⟩ + |1⟩)/√2, resulting in an equal likelihood of sampling 0 or 1 for each measured qubit (Li et al., 2021). A slightly more elaborate approach is the Entanglement Protocol (Jacak et al., 2020), in which a chain of bell states (Einstein et al., 1935) are prepared extending through the circuit depth for a similar uniform sample returned by all but the final parity qubit. Variations on these circuits may have redundancy for purposes of validation. A more resource intensive approach for sourcing randomness is known as the Sycamore Protocol, and involves preparing a circuit with randomized gates configurations at large depths, which protocol served as the basis for a milestone 2019 experiment demonstrating quantum supremacy over classical hardware (Arute et al., 2019).
There is one obstacle to complete i.i.d. randomness associated with quantum hardware to be aware of. The current generation of quantum computers available through cloud resources are still in the NISQ realm (Preskill, 2018), which refers to noisy intermediate scale quantum devices. In quantum computing, noise refers to channels of decoherence that may translate a qubit’s pure quantum state into a mixed state (Witten, 2020), which is undesirable for purposes of algorithmic fidelity. A prominent channel for decoherence may originate from the application of gates, and thus NISQ hardware may have some limit to circuit depth before noise starts to interfere with output, although such decoherence should not be a dominant feature in small circuit depths associated with random sampling. Depending on the style of qubit there will also be some fundamental coherence degradation rate. NISQ limitations can be overcome with error correction, and protocols have long been established to aggregate a set of physical qubits into a collective fault tolerant logical qubit, like the Shor code which aggregates 9 physical qubits into 1 logical qubit (Shor, 1995). The hurdle is that an architecture has to first reach a sufficient quality of qubit and fidelity of gates and measurements (Bharti et al., 2021), which thresholds vary by implementation.
We expect that the contributions of Zeno gate control circuits (Blumenthal et al., 2021) will benefit from injecting i.i.d. stochasticity into adjacent features to increase prevalence of conical intersections. Injecting known noise profiles to input features of inference means it can be conducted in a manner benign to classical model performance.
6. Intrinsic Dimensions
One way to think about what is taking place with the noise injections is that the perturbation vectors result in an increase to the intrinsic dimensionality of the function fd relating data to labels, where the intrinsic dimension of this function should be a subspace to the complexity of the environment. When estimating intrinsic dimension of a data set, some methods may attempt to isolate the data generating function from any adjacent sources of noise (Granata & Carnevale, 2016), however the function fm modeled by the network will include both channels. When a deep network learns a representation of the transformation function, the model’s intrinsic dimensionality can be expected to adhere closer to the dimensionality of the function as opposed to the complexity of the domain (Cloninger & Klock, 2021).
An intuitive interpretation could be that minimizing the distribution shift between fd and fm with a comparable intrinsic dimension may benefit performance, however the benefits of data augmentation suggest that distribution manipulations that increase the intrinsic dimension may be constructive to a model’s ability to generalize (Marcu & Prügel-Bennett, 2021). One of the benefits of the tabular modality in comparison to image domain is that training data sets are often capable at reasonable scales to fully capture characteristics of the function fd available within the observed features. In a benchmarking experiment for tabular data augmentation by gaussian noise injections to training features in a deep learning application (Teague, 2020a), it was found that such noise augmentation was mostly benign to model performance in a fully represented data set, but was increasingly beneficial as the training data scale before augmentation was reduced to simulate underrepresentation. We speculate this could be from in cases of underrepresented training data, a modeled function fm will capture representations of spurious dimensions associated with gaps in the fidelity of fd from underrepresented training data, and that the introduction of noise augmentation serves to dampen the modeling of spurious dimensions by diverting complexity capacity of the network from less tractable spurious dimensions associated with gaps in fidelity from underrepresented data to tractable noise dimensions. Thus even though the noise augmentation is increasing the intrinsic dimension of fd, it is doing so in a manner that improves generalization performance. Further, the types of noise applied, when in some manner aligned or correlated with the data generating function, will not have a fully additive increase to intrinsic dimension — this is why augmentation with common noise profiles like Gaussian, which arise naturally under the central limit theorem, will likely perform better than some exotic variant — similar to how in image modality is is common to augment by mirroring images between left and right as opposed to up and down.
Having established that noise injection will increase the intrinsic dimension of fd, it is interesting that even though the modeled fm should also be higher, the resulting stochastic regularization may actually dampen dimensionality. (Camuto et al., 2020) demonstrated that the effect of stochastic regularization realized from Gaussian noise can be related to the Fourier representation of the modeled function fm by considering it’s form in Sobolev space and modeling the data as a density function, which demonstrated that the noise injections to training data produces a regularization that penalizes higher frequency terms, resulting in a modeled function fm with lower-frequency components, and further that this dampening appeared to be recursive through layers, such that deeper layers realized lower frequency components compared to earlier. Such dampening of Fourier frequencies would be consistent with a reduced intrinsic dimensionality.
The question of Fourier domain representation of the modeled function is actually relevant to other aspects of quantum computing. In variational quantum algorithms (Cerezo et al., 2021), parameterized gates are tuned from a gradient signal with a classical optimizer, and such parameterized quantum circuits can even be integrated as modules mixed with classical neural networks as a combined quantum neural network to be collectively trained with a common gradient signal (Broughton et al., 2021). There is an interesting distinction to be made between classical learning and variational quantum circuits associated with neutrality to data representations. In deep learning (Goodfellow et al., 2016) some people consider the practice of feature engineering as obsolete, as deep networks are universal function approximators. Performance of variational quantum circuits are more tied to data encoding strategies. The tuning of gates are actually learning Fourier coefficients, but they are limited to learning coefficients of frequencies that are represented in the data encoding space. Thus one important lever to improve the performance of variational quantum circuits is by enhancing the frequency spectrum of the data encodings (Schuld et al., 2021).
The relevance to application of stochastic perturbations is that since stochastic regularization is actually dampening the Fourier frequencies, an added benefit of non-deterministic inference is that the noise injections to test data should have the result of recovering some of the dampened frequencies in space of inference, which may become beneficial in classical machine learning applications adjacent to quantum computing applications, like for those mixed modules between classical and quantum learning that may be configured in a quantum neural network.
7. Related Work
The integration of stochasticity into a neural network supervised learning workflow is a long established practice. An early example included the use of noise injected to a hidden layer to derive a gradient signal (Le Cun et al., 1989) as an alternative to backpropagation (Rumelhart et al., 1986). In modern practice stochasticity can be integrated into training in several forms. For example stochastic effects of dropout (Srivastava et al., 2014), batch normalization (Ioffe & Szegedy, 2015), data augmentation (Perez & Wang, 2017), stochastic activation functions (Ghodsi et al., 2021), perturbed gradient updates (Zhou et al., 2019), or even stochastic gradient descent itself (Smith et al., 2020) may introduce an implicit regularization into training, where implicit regularization refers to the notion that approximate computation can implicitly lead to statistical regularization (Derezinski et al., 2020).
The injection of noise into training data features may realize a similar benefit. Training feature noise can reduce sensitivity to variations in input and improve generalization (Matsuoka, 1992) with an effect equivalent to adding a regularization term to the loss function (Bishop, 1995). Noise injections to training features result in smoother fitness landscape minima and reduced model complexity, with models that have lower frequencies in the Fourier domain (Camuto et al., 2020) and an increased threshold for number of parameters needed to reach the overparameterization regime (Dhifallah & Lu, 2021) — which we speculate is associated with additional perturbation vectors causing an increase to the intrinsic dimension of the modeled transformation function in a manner similar to data augmentation’s impact to intrinsic dimension (Marcu & Prügel-Bennett, 2021).
The injection of noise into training features has been shown to improve model robustness, with reduced exposure to adversarial examples (Zantedeschi et al., 2017; Kannan et al., 2018), and noise injected to inference features may further protect against adversarial examples (Cohen et al., 2019). Adversarial examples can be considered a form of worst-case noise profile in comparison to the benign properties of random noise (Fawzi et al., 2016) and one can expect orders of magnitude more robustness to random noise than adversarial examples (Franceschi et al., 2018). One of the premises of this work is that injected inference feature noise with a known isotropic profile can be mitigated with corresponding training feature noise profile to reduce performance degradation from the practice, where injected inference feature noise may thus be a robust protection against adversarial examples. In cases where noise with an unknown profile is expected in inference features, regularization can help to mitigate the impact (Webb, 1994).
Label noise is a special case in comparison to feature noise, and may significantly increase the scale of training data needed to achieve comparable performance (Ng, 2021), although intentional label noise injections may have potential to help offset inherent label noise (Chen et al., 2021).
Integration of stochasticity can be tailored to architectures for autoencoders (Poole et al., 2014), reinforcement learning (Igl et al., 2019), recurrent networks (Lim et al., 2021), convolutional networks (Zeiler & Fergus, 2013), and other domains. Stochastic noise is commonly applied as a channel for training data augmentation in the image modality (Shorten & Khoshgoftaar, 2019). Feature noise in training may serve as a resource for masking training data properties from recovery in inference, aka differential privacy (Dwork et al., 2017). We expect that elements of stochasticity may also be helpful for model perturbations in the aggregation of ensembles (Dietterich, 2000).
Feature noise injections have mostly positive influence from the associated regularization effect, although with increasing overparameterization dropout may be expected as a more impactful stochastic regularizer (Dhifallah & Lu, 2021). However it should be noted that there are potential negative impacts to fairness considerations. One possible consequence of the practice is that different segments of a feature set corresponding to categories in an adjacent protected feature may be impacted more than others owing to a diversity in segment distributions in comparison to a common noise profile, which may contribute to loss discrepancy between categories of that protected feature (Khani & Liang, 2020) without mitigation [Appendix G.3]. Injecting noise directly into into protected attributes may also have fairness consequences, although when there is a known noise profile there are methods available to mitigate within the loss function (Celis et al., 2021).
As a related tangent, in causal inference (Pearl, 2019) an approach for identifying causal direction makes use of independent component analysis (ICA) (Hyvärinen & Oja, 2000), which recovers independent components from a given signal (Richard et al., 2021). (Shimizu et al., 2006) suggests that for linear ICA a distinction may be warranted between noise of different profiles, as Gaussian perturbation vectors are exceptions to causal inference’s ability to detect direction of graph structures. In the context of stochastic perturbations, we suspect this might be a positive property of gaussian noise in comparison to other noise profiles, as it won’t influence directional derivations from other non gaussian vectors. This gaussian exception appears to vanish when non-linear ICA is performed with interventions for non-stationarity (Hyvärinen et al., 2019). It should be noted that the output of non-deterministic inference will likely have a non-symmetric noise distribution of exotic nature based on properties of the model, and any downstream use of causal inference may become exposed to that profile.
8. Benchmarking
A series of sensitivity analysis trials were conducted to evaluate scenarios for noise injected to training data, test data, or both while varying parameter settings [Appendix J, K, L, M]. The trials were repeated in a few learning frameworks appropriate for tabular modality, including neural networks via the Fastai library (Howard & Gugger, 2020) (with four dense layers and width equal to feature count), cat boosting via the Catboost library (Dorogush et al., 2018), and gradient boosting with XGBoost (Chen & Guestrin, 2016).
8.1 Neural Networks
The neural network [Appendix K] had a material performance benefit from injection of distribution sampled noise into training numeric features, which had the added benefit of making the model robust to corresponding noise injections into test features [Fig 2]. Categoric injections resembled a linear degradation of performance with increasing noise profile. There was a performance degradation from injections to test data in isolation, but when both were applied the performance profile was very similar between injecting just to training data verses injecting to both train and test. The exception was for numeric injections of swap noise, which had the linear degradation profile resembling the categoric noise. Neural networks were the only case demonstrating regularization from training noise injections.
For numeric injections, there did not appear to be a noticeable difference in performance when comparing Gaussian and Laplace noise, suggesting that in non-deterministic inference the exposure to a wider range of inference scenarios from thicker tails in the Laplace noise distribution, as may be desirable in some applications, was neutral compared to thin tailed distributions. The performance sensitivity profile from increasing the numeric distribution scaling appeared very similar to the performance sensitivity profile from increasing ratio of injected entries by the Bernoulli sampling. An interesting finding was to what extent the preceding Bernoulli sampling (which resulted in only a sampled ratio of entries receiving noise injections) increased the model’s tolerance for increase scale of noise distribution [Fig 3].

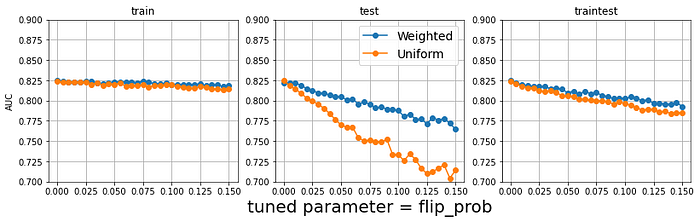

8.2 Cat Boosting
Cat boosting [Appendix L] tolerated training data injections better than gradient boosting, and injections to both train and test data closely resembled injections to just test data.
8.3 Gradient Boosting
Gradient boosting [Appendix M] demonstrated some material distinctions in comparison to the neural network [Fig 4, 5]. Instead of training data injections benefiting performance, it actually degraded, and the traintest scenario resembled the train scenario. The strongest performance came from injections only to the test features for inference, which for the numeric injections models were robust to mild noise profiles. This suggests that non-deterministic inference can be integrated directly into an existing gradient boosting pipeline with a manageable primary performance impact, which impact, without the regularizing effect from training available to neural networks, will be in play for gradient boosting in the tradeoffs between balancing a performance metric and realizing non-determinism.



9. Conclusion
This paper has surveyed considerations associated with non-deterministic inference by way of injections of stochastic perturbations into the features of a tabular data set. Prior work of tabular noise injections has mostly focused on benefits to training, we focused on injections of noise to features passed to inference for purposes of non-determinism. Benchmarks suggest that model performance varies by learning paradigm, with neural networks having a positive impact to the performance metric when corresponding symmetric distribution sampled injections are incorporated into both train and test numeric features, and gradient boosting having only small performance impact when numeric distribution sampled injections are only incorporated into test features for inference, suggesting that stochastic perturbations could be integrated into existing data pipelines for prior trained gradient boosting models.
We offer the Automunge library for tabular preprocessing as a resource for this practice, which in addition to automating data preparations for tabular learning by numeric encodings and missing data infill also serves as a platform for engineering custom pipelines of univariate transformations fit to properties of a train set. The library includes support for channeling random sampling or entropy seeds sourced from quantum circuits into stochastic perturbations, which may benefit non-deterministic inference from a more pure randomness profile in comparison to pseudo random number generators. Full documentation and tutorials are online at automunge.com and expanded on in [Appendix A].

Acknowledgments
A thank you owed to those facilitators behind Stack Overflow, Python, Numpy, Scikit-Learn, Scipy Stats, PyPI, GitHub, Colaboratory, Anaconda, VSCode, and Jupyter. Special thanks to the team at Pandas.
References
Anis, M. S., Abraham, H., AduOffei, Agarwal, R., Agliardi, G., Aharoni, M., Akhalwaya, I. Y., Aleksandrowicz, G., Alexander, T., Amy, M., Anagolum, S., Arbel, E., Asfaw, A., Athalye, A., Avkhadiev, A., Azaustre, C., Bhole, P., Banerjee, A., Banerjee, S., and the rest of the Qiskit community. Qiskit: An open-source framework for quantum computing, 2021. URL https://qiskit.org/.
Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J., Barends, R., Biswas, R., Boixo, S., Brandao, F., Buell, D., Burkett, B., Chen, Y., Chen, Z., Chiaro, B., Collins, R., Courtney, W., Dunsworth, A., Farhi, E., Foxen, B., and Martinis, J. Quantum supremacy using a programmable superconducting processor. Nature, 574:505–510, 10 2019. doi: 10.1038/s41586–019–1666–5. URL https: //doi.org/10.1038/s41586–019–1666–5.
Bharti, K., Cervera-Lierta, A., Kyaw, T. H., Haug, T., Alperin-Lea, S., Anand, A., Degroote, M., Heimonen, H., Kottmann, J. S., Menke, T., Mok, W.-K., Sim, S., Kwek, L.-C., and Aspuru-Guzik, A. Noisy intermediate-scale quantum (nisq) algorithms, 2021. URL https: //arxiv.org/abs/2101.08448.
Bishop, C. M. Training with noise is equivalent to tikhonov regularization. Neural Computation, 7(1): 108–116, 1995. doi: 10.1162/neco.1995.7.1.108. URL https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/bishop-tikhonov-nc-95.pdf.
Blumenthal, E., Mor, C., Diringer, A. A., Martin, L. S., Lewalle, P., Burgarth, D., Whaley, K. B., and Hacohen-Gourgy, S. Demonstration of universal control between non-interacting qubits using the Quantum Zeno effect, 2021. URL https://arxiv.org/abs/2108.08549.
Broughton, M., Verdon, G., McCourt, T., Martinez, A. J., Yoo, J. H., Isakov, S. V., Massey, P., Halavati, R., Niu, M. Y., Zlokapa, A., Peters, E., Lockwood, O., Skolik, A., Jerbi, S., Dunjko, V., Leib, M., Streif, M., Dollen, D. V., Chen, H., Cao, S., Wiersema, R., Huang, H.-Y., McClean, J. R., Babbush, R., Boixo, S., Bacon, D., Ho, A. K., Neven, H., and Mohseni, M. Tensorflow quantum: A software framework for quantum machine learning, 2021. URL https://arxiv.org/abs/2003.02989.
Camuto, A., Willetts, M., Simsekli, U., Roberts, S. J., and Holmes, C. C. Explicit regularisation in gaussian noise injections. In Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M. F., and Lin, H. (eds.), Advances in Neural Information Processing Systems, volume 33, pp. 16603–16614. Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper/2020/file/ c16a5320fa475530d9583c34fd356ef5-Paper.pdf.
Celis, L. E., Huang, L., Keswani, V., and Vishnoi, N. K. Fair classification with noisy protected attributes: A framework with provable guarantees. In Meila, M. and Zhang, T. (eds.), Proceedings of the 38th International Conference on Machine Learning, volume 139 of Proceedings of Machine Learning Research, pp. 1349–1361. PMLR, 18–24 Jul 2021. URL https://proceedings.mlr.press/v139/celis21a.html.
Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C., Endo, S., Fujii, K., McClean, J. R., Mitarai, K., Yuan, X., Cincio, L., and et al. Variational quantum algorithms. Nature Reviews Physics, 3(9): 625–644, Aug 2021. ISSN 2522–5820. doi: 10.1038/ s42254–021–00348–9. URL http://dx.doi.org/10.1038/s42254–021–00348–9.
Chen, P., Chen, G., Ye, J., jingwei zhao, and Heng, P.-A. Noise against noise: stochastic label noise helps combat inherent label noise. In International Conference on Learning Representations, 2021. URL https://openreview.net/forum?id=80FMcTSZ6J0.
Chen, T. and Guestrin, C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug 2016. doi: 10.1145/2939672.2939785. URL http://dx.doi.org/10.1145/2939672.2939785.
Cloninger, A. and Klock, T. A deep network construction that adapts to intrinsic dimensionality beyond the domain, 2021. URL https://arxiv.org/abs/2008.02545.
Cohen, J., Rosenfeld, E., and Kolter, Z. Certified adversarial robustness via randomized smoothing. In Chaudhuri, K. and Salakhutdinov, R. (eds.), Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pp. 1310–1320. PMLR, 09–15 Jun 2019. URL https://proceedings.mlr.press/v97/cohen19c.html.
Cook, J. D. Normal approximation to laplace distribution?, Feb 2019. URL https://www.johndcook.com/blog/2019/02/05/.
Derezinski, M., Liang, F. T., and Mahoney, M. W. Exact expressions for double descent and implicit regularization via surrogate random design. In Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M. F., and Lin, H. (eds.), Advances in Neural Information Processing Systems, volume 33, pp. 5152–5164. Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper/2020/file/37740d59bb0eb7b4493725b2e0e5289b-Paper.pdf.
Dhifallah, O. and Lu, Y. On the inherent regularization effects of noise injection during training. In Meila, M. and Zhang, T. (eds.), Proceedings of the 38th International Conference on Machine Learning, volume 139 of Proceedings of Machine Learning Research, pp. 2665–2675. PMLR, 18–24 Jul 2021. URL https://proceedings.mlr.press/v139/dhifallah21a.html.
Dietterich, T. G. Ensemble methods in machine learning. In Multiple Classifier Systems, LBCS-1857, pp. 1–15. Springer, 2000. URL https://web.engr.oregonstate.edu/~tgd/publications/mcs-ensembles.pdf.
Dorogush, A. V., Ershov, V., and Gulin, A. Catboost: gradient boosting with categorical features support, 2018. URL https://arxiv.org/abs/1810.11363.
Dwork, C., McSherry, F., Nissim, K., and Smith, A. Calibrating noise to sensitivity in private data analysis. Journal of Privacy and Confidentiality, 7(3): 17–51, May 2017. doi: 10.29012/jpc.v7i3.405. URL https://journalprivacyconfidentiality.org/index.php/jpc/article/view/405.
Einstein, A., Podolsky, B., and Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47 (10):777–780, May 1935. doi: 10.1103/PhysRev.47. 777. URL https://journals.aps.org/pr/abstract/10.1103/PhysRev.47.777.
Fawzi, A., Moosavi-Dezfooli, S.-M., and Frossard, P. Robustness of classifiers: From adversarial to random noise. In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS’16, pp. 1632–1640, Red Hook, NY, USA, 2016. Curran Associates Inc. ISBN 9781510838819. URL https://proceedings.neurips.cc/paper/2016/file/7ce3284b743aefde80ffd9aec500e085-Paper.pdf.
Franceschi, J.-Y., Fawzi, A., and Fawzi, O. Robustness of classifiers to uniform lp and gaussian noise. In Storkey, A. and Perez-Cruz, F. (eds.), Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, volume 84 of Proceedings of Machine Learning Research, pp. 1280–1288. PMLR, 09–11 Apr 2018.URL https://proceedings.mlr.press/v84/franceschi18a.html.
Ghodsi, Z., Jha, N. K., Reagen, B., and Garg, S. Circa: Stochastic ReLUs for private deep learning. In Beygelzimer, A., Dauphin, Y., Liang, P., and Vaughan, J. W. (eds.), Advances in Neural Information Processing Systems, 2021. URL https://openreview.net/forum?id=_n59kgzSFef.
Goodfellow, I. J., Bengio, Y., and Courville, A. Deep Learning. MIT Press, Cambridge, MA, USA, 2016. http://www.deeplearningbook.org.
Granata, D. and Carnevale, V. Accurate estimation of the intrinsic dimension using graph distances: Unraveling the geometric complexity of datasets. Scientific Reports, 6: 31377, 08 2016. doi: 10.1038/srep31377. URL https://rdcu.be/cFOZg.
Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer, S., van Kerkwijk, M. H., Brett, M., Haldane, A., Fernández del R ́ıo, J., Wiebe, M., Peterson, P., Gérard-Marchant, P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi, H., Gohlke, C., and Oliphant, T. E. Array programming with NumPy. Nature, 585:357–362, 2020. doi: 10.1038/s41586–020–2649–2. URL https://rdcu.be/cFPe6.
Howard, J. and Gugger, S. Deep Learning for Coders with Fastai and PyTorch. O’Reilly Media, 2020. URL https://www.fast.ai/.
Hyvärinen, A. and Oja, E. Independent component analysis: algorithms and applications. Neural Networks, 13(4):411–430, 2000. ISSN 0893–6080. doi: https://doi.org/10.1016/S0893-6080(00)00026-5. URL https://www.sciencedirect.com/science/article/pii/S0893608000000265.
Hyvärinen, A., Sasaki, H., and Turner, R. Nonlinear ICA using auxiliary variables and generalized contrastive learning. In Chaudhuri, K. and Sugiyama, M. (eds.), Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, volume 89 of Proceedings of Machine Learning Research, pp. 859–868. PMLR, 16–18 Apr 2019. URL https://proceedings.mlr.press/v89/hyvarinen19a.html.
Igl, M., Ciosek, K., Li, Y., Tschiatschek, S., Zhang, C., Devlin, S., and Hofmann, K. Generalization in reinforcement learning with selective noise injection and information bottleneck. In Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., and Garnett, R. (eds.), Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019. URL https://proceedings.neurips.cc/paper/2019/file/e2ccf95a7f2e1878fcafc8376649b6e8-Paper.pdf.
Ioffe, S. and Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Bach, F. and Blei, D. (eds.), Proceedings of the 32nd International Conference on Machine Learning, volume 37 of Proceedings of Machine Learning Research, pp. 448–456, Lille, France, 07–09 Jul 2015. PMLR. URL https://proceedings.mlr.press/v37/ioffe15.html.
Jacak, J. E., Jacak, W. A., Donderowicz, W. A., and Jacak, L. Quantum random number generators with entanglement for public randomness testing. Sci Rep., 10(1):8101, 2020. doi: 10.1038/s41598–019–56706–2. URL https://rdcu.be/cFPfz.
Kadra, A., Lindauer, M., Hutter, F., and Grabocka, J. Well-tuned simple nets excel on tabular datasets. In Beygelzimer, A., Dauphin, Y., Liang, P., and Vaughan, J. W. (eds.), Advances in Neural Information Processing Systems, 2021. URL https://openreview.net/forum?id=d3k38LTDCyO.
Kannan, H., Kurakin, A., and Goodfellow, I. Adversarial logit pairing, 2018. URL https://arxiv.org/abs/1803.06373.
Khani, F. and Liang, P. Feature noise induces loss discrepancy across groups. In III, H. D. and Singh, A. (eds.), Proceedings of the 37th International Conference on Machine Learning, volume 119 of Proceedings of Machine Learning Research, pp. 5209–5219. PMLR, 13–18 Jul 2020. URL https://proceedings.mlr.press/v119/khani20a.html.
Le Cun, Y., Galland, C., and Hinton, G. E. Gemini: Gradient estimation through matrix inversion after noise injection. In Touretzky, D. (ed.), Advances in Neural Information Processing Systems, volume 1. Morgan-Kaufmann, 1989. URL https://proceedings.neurips.cc/paper/1988/file/a0a080f42e6f13b3a2df133f073095dd-Paper.pdf.
Li, Y., Fei, Y., Wang, W., Meng, X., Wang, H., Duan, Q., and Ma, Z. Quantum random number generator using a cloud superconducting quantum computer based on source-independent protocol. Scientific Reports, 11, 12 2021. doi: https://doi.org/10.1038/s41598-021-03286-9. URL https://rdcu.be/cFPgO.
Lim, S. H., Erichson, N. B., Hodgkinson, L., and Mahoney, M. W. Noisy recurrent neural networks. In Beygelzimer, A., Dauphin, Y., Liang, P., and Vaughan, J. W. (eds.), Advances in Neural Information Processing Systems, 2021. URL https://openreview.net/forum?id=mf9XiRCEgZu.
Marcu, A. and Prügel-Bennett, A. On data-centric myths. In Data-Centric AI Workshop (NeurIPS), 2021. URL https://arxiv.org/abs/2111.11514.
Matsumoto, M. and Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul., 8(1):3–30, jan 1998. ISSN 1049–3301. doi: 10.1145/272991.272995. URL https://doi.org/10.1145/272991.272995.
Matsuoka, K. Noise injection into inputs in back-propagation learning. IEEE Transactions on Systems, Man, and Cybernetics, 22(3):436–440, 1992. doi: 10.1109/21.155944. URL https://ieeexplore.ieee.org/document/155944.
McKinney, W. Data structures for statistical computing in python. Proceedings of the 9th Python in Science Conference, pp. 51–56, 2010. URL http: //conference.scipy.org/proceedings/ scipy2010/pdfs/mckinney.pdf.
Ng, A. MLOps: From model-centric to data-centric AI, 2021. URL https://youtu.be/06-AZXmwHjo.
Nielsen, M. A. and Chuang, I. L. Quantum Computation and Quantum Information. Cambridge University Press, 2010. URL https://dl.acm.org/doi/10.5555/1972505.
O’Neill, M. E. PCG : A family of simple fast space-efficient statistically good algorithms for random number generation. 2014. URL https://www.pcg-random.org/paper.html.
Pearl, J. The seven tools of causal inference, with reflections on machine learning. Communications of the ACM, 62(3): 54–60, 2019. URL https://dl.acm.org/doi/10.1145/3241036.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Édouard Duchesnay. Scikit-learn: Machine learning in python. Journal of Machine Learning Research, 12:2825–2830, 2011. URL http://jmlr.org/papers/v12/pedregosa11a.html.
Perez, L. and Wang, J. The effectiveness of data augmentation in image classification using deep learning, 2017. URL https://arxiv.org/abs/1712.04621.
Piani, M., Mosca, M., and Neill, B. Quantum random-number generators: Practical considerations and use cases, 2021. URL https://evolutionq.com/quantum-safe-publications/qrng-report-2021-evolutionQ.pdf.
Poole, B., Sohl-Dickstein, J., and Ganguli, S. Analyzing noise in autoencoders and deep networks. ArXiv, abs/1406.1831, 2014. URL https://arxiv.org/abs/1406.1831.
Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum, 2:79, August 2018. ISSN 2521–327X. doi: 10. 22331/q-2018–08–06–79. URL https://doi.org/10.22331/q-2018–08–06–79.
Richard, H., Ablin, P., Hyva ̈rinen, A., Gramfort, A., and Thirion, B. Adaptive multi-view ICA: Estimation of noise levels for optimal inference, 2021. URL https://arxiv.org/abs/2102.10964.
Rivero, P. Qrand. https://github.com/pedrorrivero/qrand, 2021.
Rodriguez, I. D., Bonet, B., Sardina, S., and Geffner, H. Flexible FOND planning with explicit fairness assumptions, 2021. URL https://arxiv.org/abs/2103.08391.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. Learning Representations by Back-propagating Errors. Nature, 323(6088):533–536, 1986. doi: 10. 1038/323533a0. URL http://www.nature.com/articles/323533a0.
Schuld, M., Sweke, R., and Meyer, J. J. Effect of data encoding on the expressive power of variational quantum-machine-learning models. Physical Review A, 103(3), Mar 2021. ISSN 2469–9934. doi: 10.1103/physreva.103. 032430. URL http://dx.doi.org/10.1103/PhysRevA.103.032430.
Shannon, C. E. A mathematical theory of communication. The Bell System Technical Journal, 27:379–423, 1948. URL https://en.wikipedia.org/wiki/A_Mathematical_Theory_of_Communication.
Shimizu, S., Hoyer, P. O., Hyvärinen, A., and Kerminen, A. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(72):2003– 2030, 2006. URL http://jmlr.org/papers/v7/shimizu06a.html.
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A, 52: R2493–R2496, Oct 1995. doi: 10.1103/PhysRevA.52. R2493. URL https://link.aps.org/doi/10.1103/PhysRevA.52.R2493.
Shorten, C. and Khoshgoftaar, T. M. A survey on image data augmentation for deep learning. Journal of Big Data, 6:1–48, 2019. URL https://rdcu.be/cFPma.
Smith, S., Elsen, E., and De, S. On the generalization benefit of noise in stochastic gradient descent. In III, H. D. and Singh, A. (eds.), Proceedings of the 37th International Conference on Machine Learning, volume 119 of Proceedings of Machine Learning Research, pp. 9058–9067. PMLR, 13–18 Jul 2020. URL https://proceedings.mlr.press/v119/smith20a.html.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929–1958, 2014. URL http://jmlr.org/papers/v15/srivastava14a.html.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. Rethinking the inception architecture for computer vision. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2818–2826, 2016. doi: 10.1109/CVPR.2016.308. URL https://arxiv.org/abs/1512.00567.
Taleb, N. N. How much data do you need? An operational, pre-asymptotic metric for fat-tailedness. International Journal of Forecasting, 35(2):677–686, Apr 2019. ISSN 0169–2070. doi: 10.1016/j.ijforecast.2018. 10.003. URL http://dx.doi.org/10.1016/j.ijforecast.2018.10.003.
Taleb, N. N. Statistical Consequences of Fat Tails. STEM Academic Press, 1st edition, 2020. URL https://arxiv.org/abs/2001.10488.
Teague, N. Numeric encoding options with Automunge, 2020a. URL https://openreview.net/pdf?id=2kImxCmYBic.
Teague, N. Parsed categoric encodings with Automunge, 2020b. URL https://openreview.net/pdf?id=Dh29CAlnMW.
Teague, N. Missing data infill with Automunge, 2021a. URL https://openreview.net/pdf?id=o2tx_m7hK3t.
Teague, N. Automunge code repository, documentation, and tutorials, 2021b. URL https://github.com/Automunge/AutoMunge.
Tran, D., Kucukelbir, A., Dieng, A. B., Rudolph, M., Liang, D., and Blei, D. M. Edward: A library for probabilistic modeling, inference, and criticism, 2017. URL https://arxiv.org/abs/1610.09787.
Ucar, T., Hajiramezanali, E., and Edwards, L. Subtab: Subsetting features of tabular data for self-supervised representation learning. In Beygelzimer, A., Dauphin, Y., Liang, P., and Vaughan, J. W. (eds.), Advances in Neural Information Processing Systems, 2021. URL https://openreview.net/forum?id=vrhNQ7aYSdr.
Vesta. IEEE-CIS fraud detection data set. https://www.kaggle.com/c/ieee-fraud-detection/, 2019.
Virtanen, P., Gommers, R., Oliphant, T., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S., Brett, M., Wilson, J., Jarrod Millman, K., Mayorov, N., Nelson, A., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, ̇I., Feng, Y., Moore, E., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 17:261–272, 2020. doi: https://doi.org/10.1038/s41592-019-0686-2. URL https://rdcu.be/cFPnu.
Webb, A. Functional approximation by feedforward networks: A least-squares approach to generalization. Neural Networks, IEEE Transactions on, 5:363–371, 06 1994. doi: 10.1109/72.286908. URL https://ieeexplore.ieee.org/document/286908.
Wickham, H. Tidy data. Journal of Statistical Software, Articles, 59(10):1–23, 2014. ISSN 1548–7660. doi: 10.18637/jss.v059.i10. URL https://www.jstatsoft.org/v059/i10.
Witten, E. A mini-introduction to information theory. La Rivista del Nuovo Cimento, 43(4):187–227, Mar 2020. ISSN 1826–9850. doi: 10.1007/ s40766–020–00004–5. URL http://dx.doi.org/10.1007/s40766–020–00004–5.
Zantedeschi, V., Nicolae, M.-I., and Rawat, A. Efficient defenses against adversarial attacks. Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, 2017. URL https://arxiv.org/abs/1707.06728.
Zeiler, M. and Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. In 1st International Conference on Learning Representations, ICLR 2013, January 2013. URL https://arxiv.org/abs/1301.3557.
Zhou, M., Liu, T., Li, Y., Lin, D., Zhou, E., and Zhao, T. Toward understanding the importance of noise in training neural networks. In Chaudhuri, K. and Salakhutdinov, R. (eds.), Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pp. 7594–7602. PMLR, 09– 15 Jun 2019. URL https://proceedings.mlr.press/v97/zhou19d.html.
Intellectual Property Disclaimer
Automunge is released under GNU General Public License v3.0. Full license details available on GitHub. Contact available via automunge.com. Copyright © 2021 — All Rights Reserved. Patent Pending, including applications 16552857, 17021770
For further readings please check out the Table of Contents, Book Recommendations, and Music Recommendations. For more on Automunge: automunge.com
